How to store a graph with customized nodes?
Special thanks to: ChatGPT
A graph, usually can be conceptually described and represented with ease, alongside a straightforward
illustration. When an algorithm is explained, the audience can see quite a good elaboration with a drawing
of a graph. A graph typically consists of two parts: (1) the node in the graph and (2) the relationships between
the nodes. In the blog:
Kahn’s Algorithm for Topological Sorting we simplified the modelling and implementation of a graph,
as the graph nodes are directly represented by integers, allowing them to be used as indices of an array. Based
on that, the relationships among them (a.k.a edges) can also be easily implemented. However, in many scenarios, a node
can have certain properies, such as its degree, or for instance we would like to also store
its incident nodes. Therefore, how should we represent these customized nodes, and to represent
the whole graph?
Implementation-wise, we will use C++ as our preferred language to demonstrate how it can be done.
The core logic is to store a customized (or user-defined) node, which can be easily achieved by creating
a class, and also store the relationships with its incident nodes in the graph. This can be realized
by utilizing a dictionary (std::unordered_map and std::map in C++), having the node as key and the list
of its incident nodes as values:
struct Node{
// data and methods
};
std::unordered_map<Node, std::list<Node>> adjacencyLists;
error: call to implicitly-deleted default constructor of 'std::hash': _Hash() {}
note: default constructor of 'hash' is implicitly deleted because base class '__enum_hash' has a deleted default constructor
struct _LIBCPP_TEMPLATE_VIS hash : public __enum_hash<_Tp>
note: '__enum_hash' has been explicitly marked deleted here __enum_hash() = delete;
error: static assertion failed due to requirement 'integral_constant::value': the specified hash does not meet the Hash requirements
static_assert(__check_hash_requirements<_Key, _Hash>::value,
- A DAG contains at least one vertex with the indegree zero.
- A DAG contains at least one vertex with the outdegree zero.
Let us see an example:
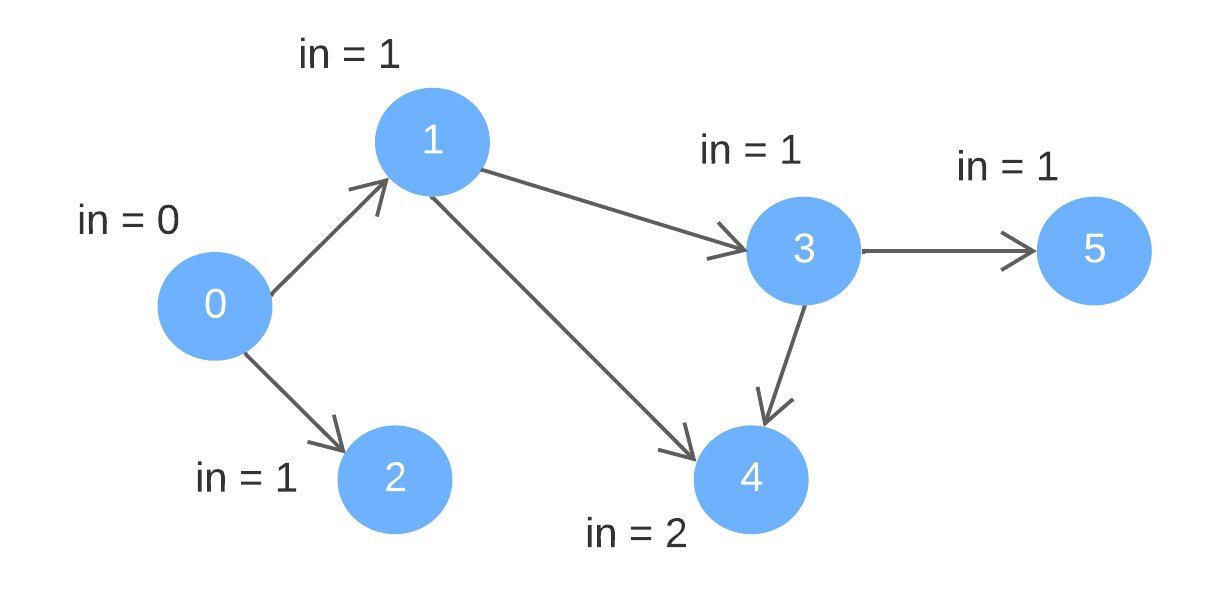
Directed edges: {0, 1}, {0, 2}, {1, 3}, {1, 4}, {3, 4}, {3, 5}
"in" represents "indegree"
Order of removal: 0, 1, 2, 3, 4, 5
A possible topological order: 0, 1, 2, 3, 4, 5
Note that the sequence is not the only possible topological order. For instance, 0, 2, 1, 3, 4, 5 is also a valid topological order.
The process of Kahn's algorithm:
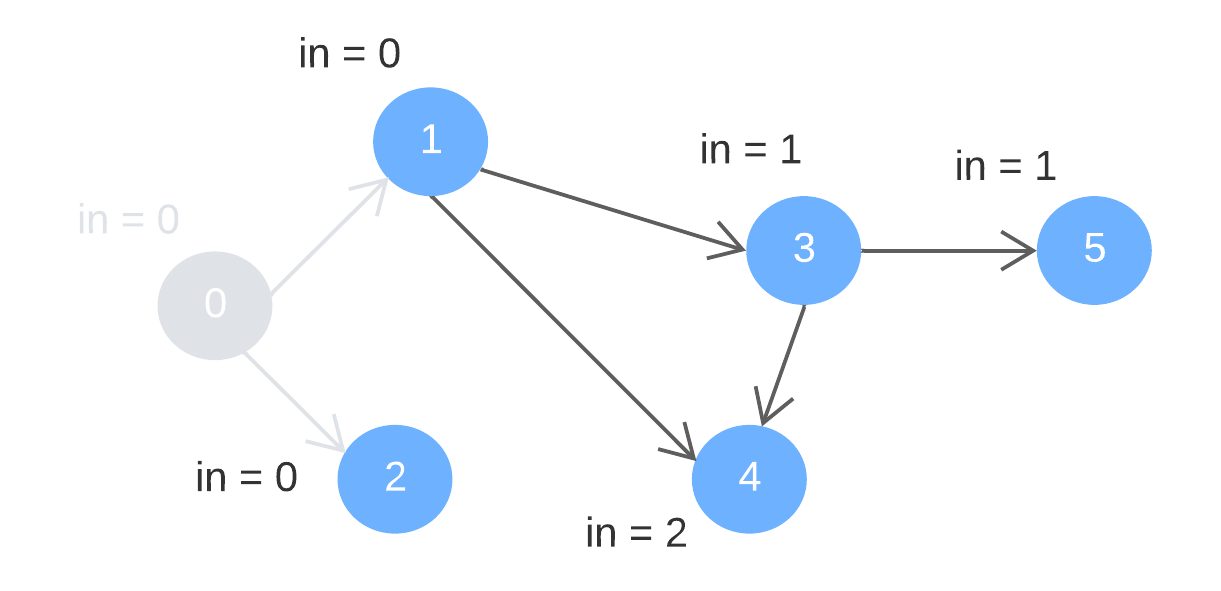
Step 1: remove node 0 (with indegree = 0) and its outward edges. Update the indegree of the deleted edges’ destination nodes (1 and 2).
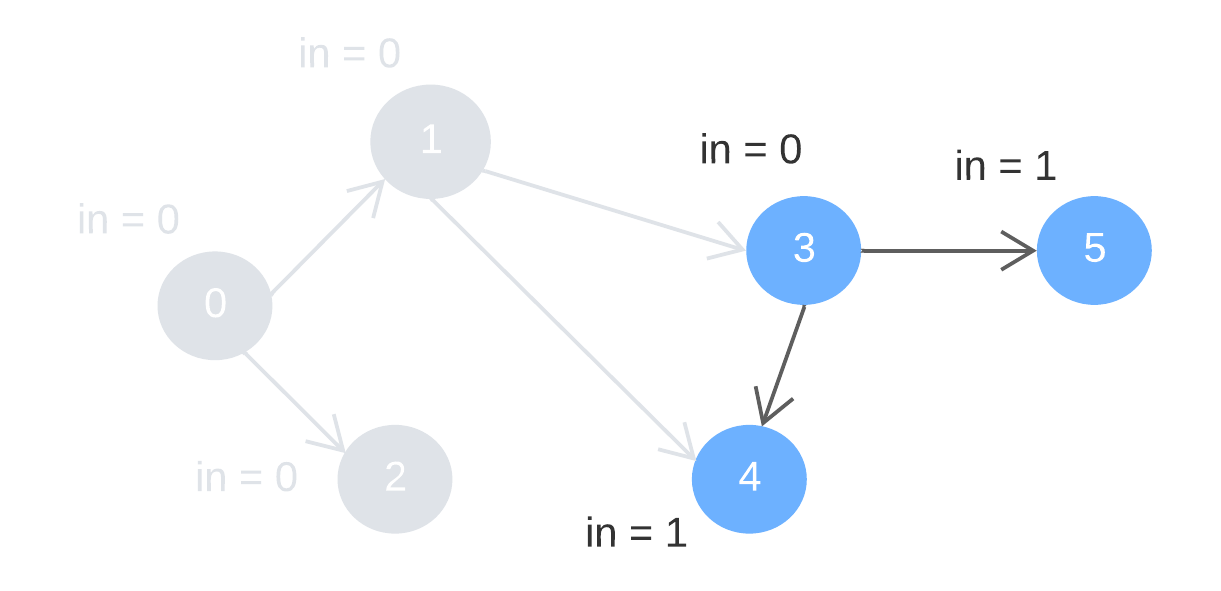
Step 2: remove node 1 and 2, alongside the outward edges. Update the indegree of node 3 and 4.
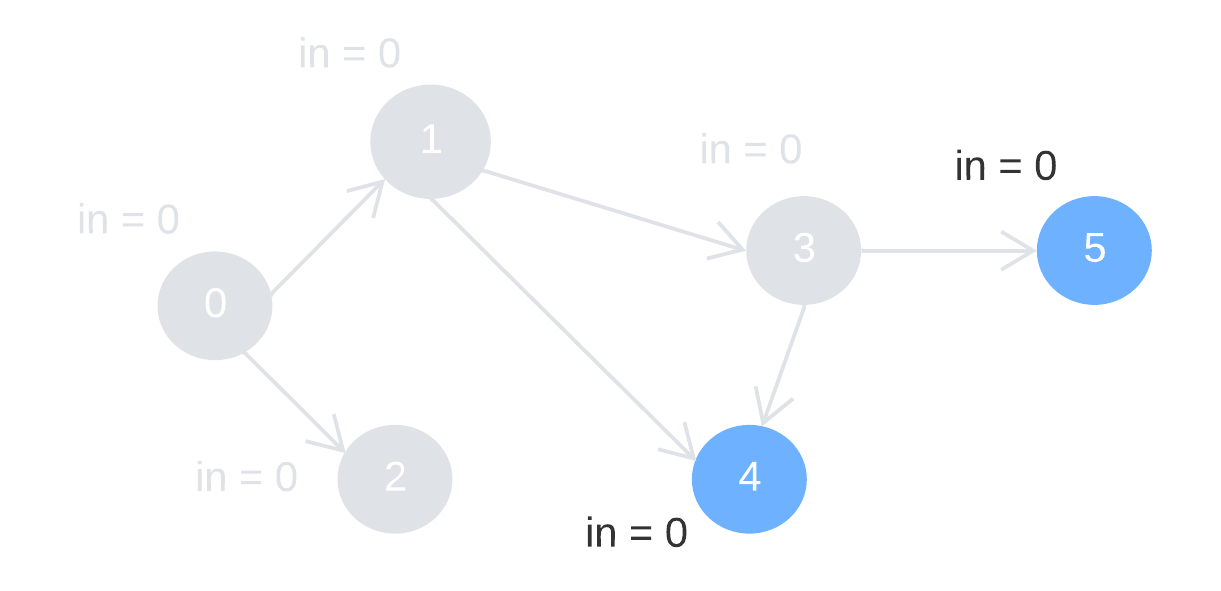
Step 3: remove node 3 and its outward edges. Update the indegree of node 4 and 5.
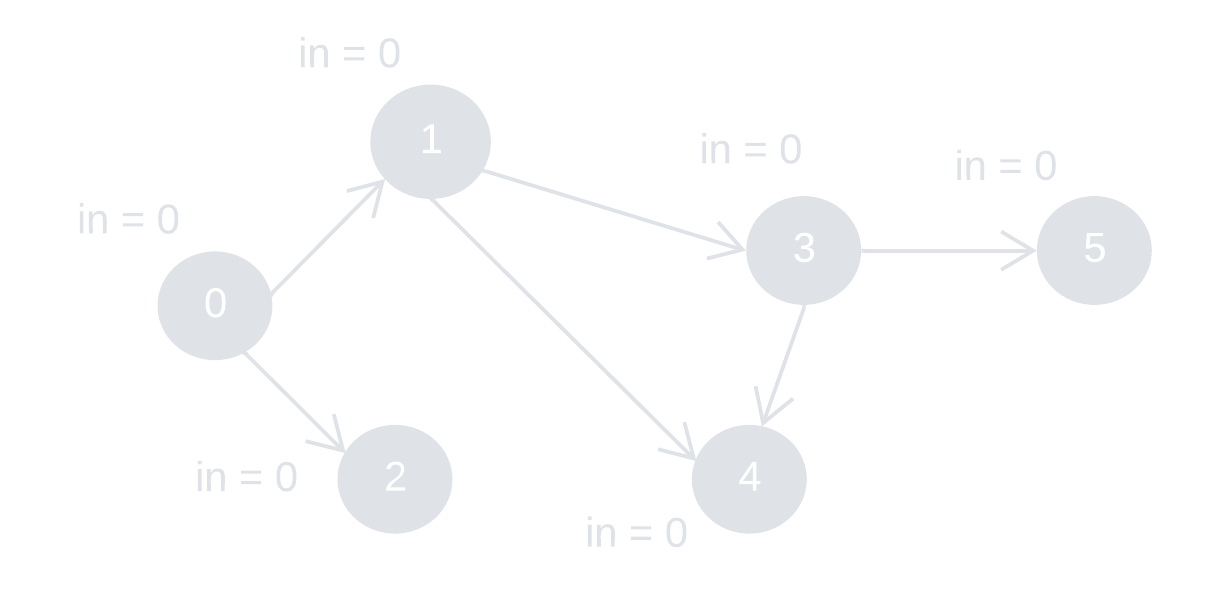
Step 4: remove node 4 and 5.
Given a DAG, denoted as G and represented with an adjacency list, the algorithm can be summarized as follows:
- Calculate the indegree for all nodes in G.
- Identify a node with an indegree of 0, indicating no incoming edges.
- Remove the identified node from G and add it to the topological ordering.
- Remove the outgoing edges from the removed node in G.
- Decrement the indegree of the connected destination nodes (those connected by the edges removed in the previous step).
- Repeat these steps until no nodes are left with zero indegree, signifying that either all nodes have been traversed or a cycle has been encountered.
// pseudo code for an example
Kahn_topological_sort(Graph G)
{
For each node in G{
Find and populate indegree[node]; // get the indegree for all the nodes in G
}
Create a stack or queue; // auxiliary data structure - as a container
Add nodes with indegree 0 to the queue;
while(node U with indegree 0 exists in the queue){
Remove U from the queue;
Remove all its outgoing edges (U, Vi) from G;
For destination vertices Vi which had their incoming edges removed{
indegree[Vi] -= 1;
}
Add new nodes with indegree 0 to the queue;
}
// determine if a topological ordering has been found
if(elements sorted = all elements)
return true or print nodes in topologically sorted order;
else
return false or prompt that no topological ordering exists (e.g. there exists rings in G)
}
Now let's implement it using C++, the very first thing is to design a data structure to store a graph.
For the purpose of simplfying the code, we might as well consider representing the graph nodes using integers, numbering from 0 to a specific value. We can then use these integers as array indices. Consider the following example:
node_array[0] = {1, 2};
To store our graph, we can make use of a 2D array, often referred to as an adjacencyList
vector<vector<int>> adjacencyList;
adjacencyList[0]
represents a 1D array containing the nodes incident to node 0.
The overall code is as follows:
#include <iostream>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
// Graph class - store the input graph
class Graph{
public:
Graph(int NumberOfNodes) : m_numberofNodes(NumberOfNodes){
m_adjacencyList.resize(NumberOfNodes);
m_inDegree.resize(NumberOfNodes, 0);
}
void add_directed_edges(int src, int dest){
m_adjacencyList[src].emplace_back(dest);
}
// main function: topological sort
bool topological_sort(vector<int>& sorted)
{
auto indegree_copy = m_inDegree; // save a copy of the indegree vector
// store all the nodes with no incoming edges
queue nodes_with_zero_indegree;
for(int i = 0; i < m_numberofNodes; ++i)
{
if(m_inDegree[i] == 0)nodes_with_zero_indegree.push(i);
}
// process - while the queue is not empty
while(!nodes_with_zero_indegree.empty())
{
auto current_zero_node = nodes_with_zero_indegree.front();
nodes_with_zero_indegree.pop(); // delete the node with zero indegree
sorted.emplace_back(current_zero_node); // add it to the sorted list
// alter the graph: delete the incident edges and update the indegree
// of the incident nodes connected to current_zero_node
for(auto const& dest_node : m_adjacencyList[current_zero_node])
{
// delete the directed edge: current_zero_node -> dest_node
// meaning the indegree of the dest node decrements by 1
--m_inDegree[dest_node];
// if the updated indegree of dest node is now zero
// add it to the nodes_with_zero_indegree queue
if(m_inDegree[dest_node] == 0) nodes_with_zero_indegree.push(dest_node);
} // end for
} // end while: while the queue is not empty
// a cycle was encountered - if the sorting is done but not all input nodes have been sorted
if((int)sorted.size() != m_numberofNodes)return false;
// successfully sorted
return true;
}
void print_graph() {
for(int i = 0; i < m_adjacencyList.size(); ++i)
{
if(m_adjacencyList[i].size() != 0)
{
std::cout << "Node " << i << " -> ";
for(const auto& node : m_adjacencyList[i])
{
std::cout << node << " ";
}
std::cout << std::endl;
}
}
}
protected:
int m_numberofNodes;
vector<vector<int>> m_adjacencyList;
vector<int> m_inDegree;
};
int main() {
int n = 6;
Graph graph(n);
graph.add_directed_edges(0, 1);
graph.add_directed_edges(0, 2);
graph.add_directed_edges(1, 2);
graph.add_directed_edges(2, 3);
graph.add_directed_edges(1, 4);
graph.add_directed_edges(5, 3);
graph.add_directed_edges(4, 5);
graph.print_graph();
vector<int> sorted;
sorted.reserve(n);
if(graph.topological_sort(sorted)){
std::cout << "sorted done, the topological ordering is: " << std::endl;
for(auto const& node : sorted)std::cout << node << " ";
std::cout << std::endl;
}else{
std::cout << "topological sorting is not possible as the graph is not acyclic" << std::endl;
}
return 0;
}