Kahn’s Algorithm for Topological Sorting*
*The content is intended for self-study and sharing, the original blog is: INTERVIEW KICKSTART - Kahn’s Algorithm for Topological Sorting.
In graph theory, topological sorting, often referred to as topological ordering, is primarily
employed to determine the sequence of nodes in a directed acyclic graph (DAG).
In a DAG, vertices have interdependencies due to the existance of directed edges.
For instance, given two vertices U and V, a directed edge (U, V) implies that V
can be reached from U, while the reverse is not true - U cannot be reached from V.
In this context, V is regarded to have a dependency on U.
The topological order is essentially a linear arrangement of all the vertices within a DAG.
It provides a systematic depiction of feasible sequences originating from certain vertices
and concluding at others.
Now let's delve into some fundamental yet crucial concepts regarding a DAG:
- A DAG contains at least one vertex with the indegree zero.
- A DAG contains at least one vertex with the outdegree zero.
Let us see an example:
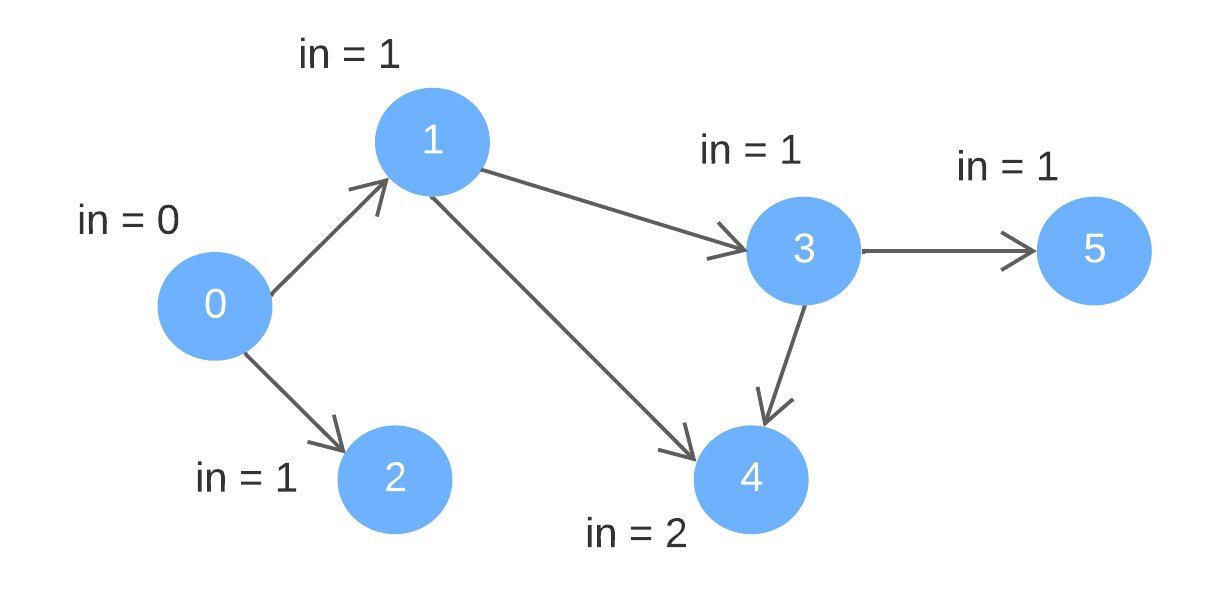
Directed edges: {0, 1}, {0, 2}, {1, 3}, {1, 4}, {3, 4}, {3, 5}
"in" represents "indegree"
Order of removal: 0, 1, 2, 3, 4, 5
A possible topological order: 0, 1, 2, 3, 4, 5
Note that the sequence is not the only possible topological order. For instance, 0, 2, 1, 3, 4, 5 is also a valid topological order.
The process of Kahn's algorithm:
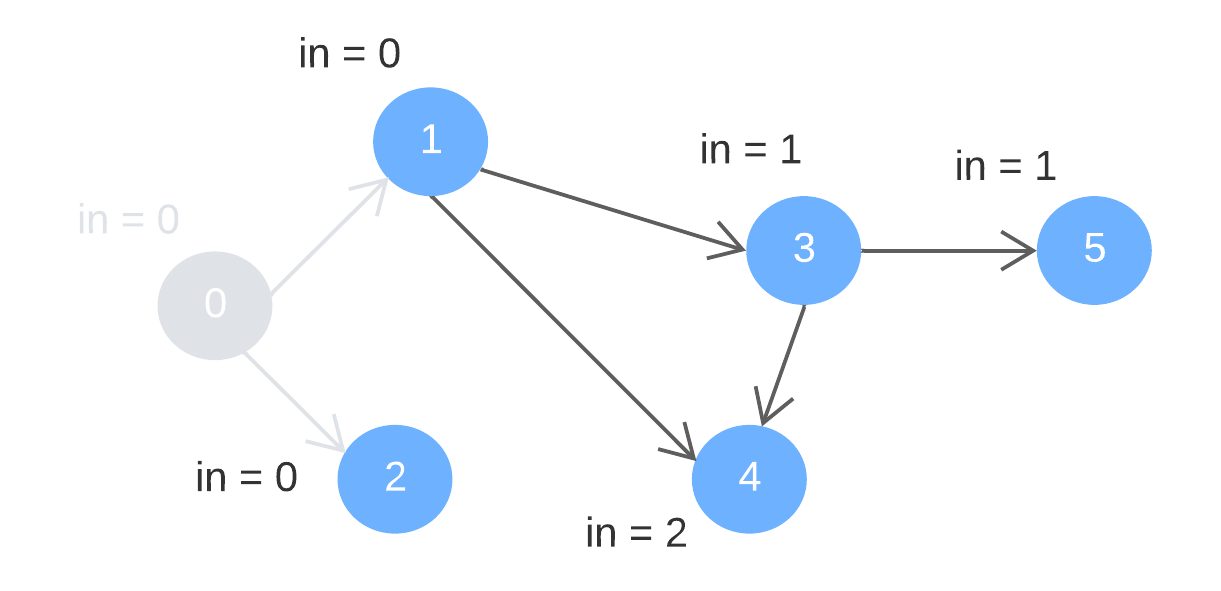
Step 1: remove node 0 (with indegree = 0) and its outward edges. Update the indegree of the deleted edges’ destination nodes (1 and 2).
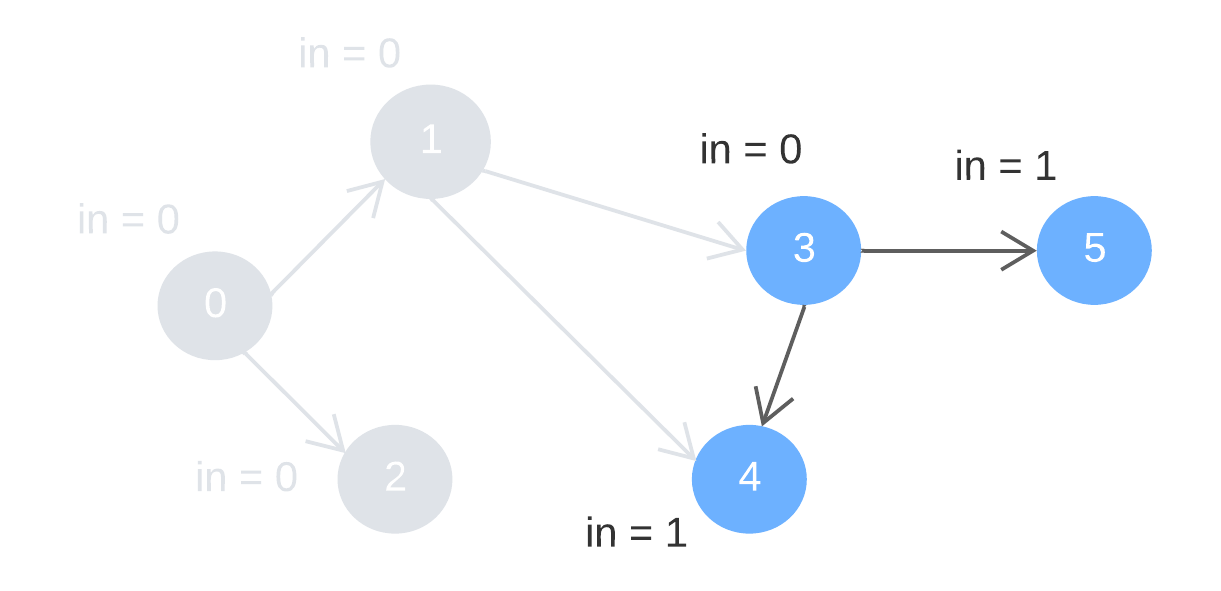
Step 2: remove node 1 and 2, alongside the outward edges. Update the indegree of node 3 and 4.
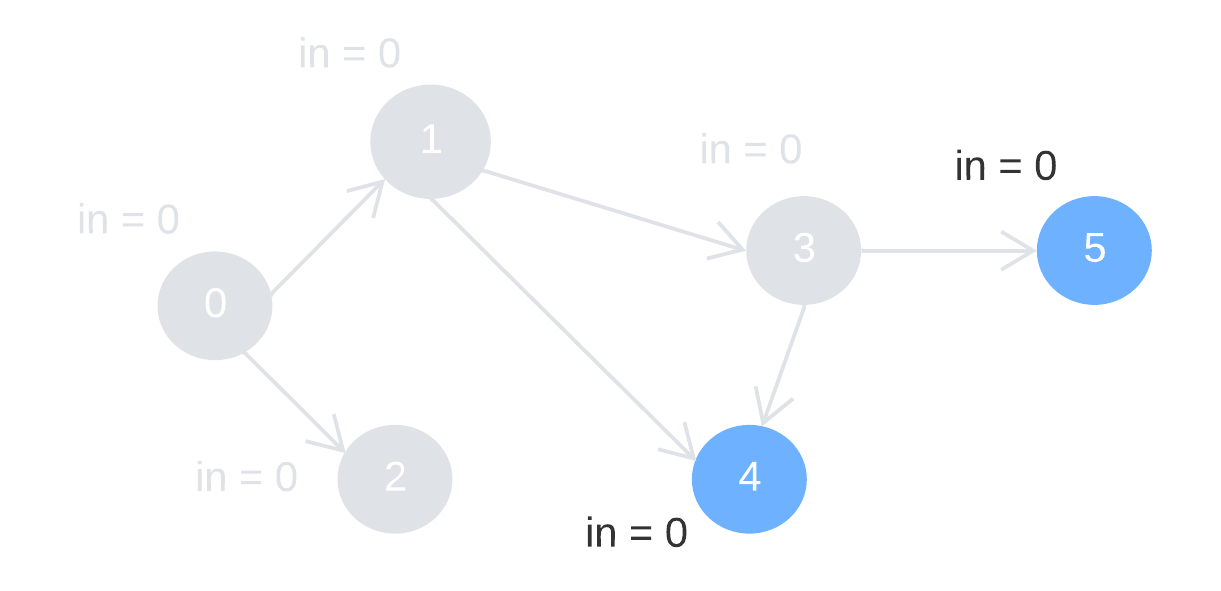
Step 3: remove node 3 and its outward edges. Update the indegree of node 4 and 5.
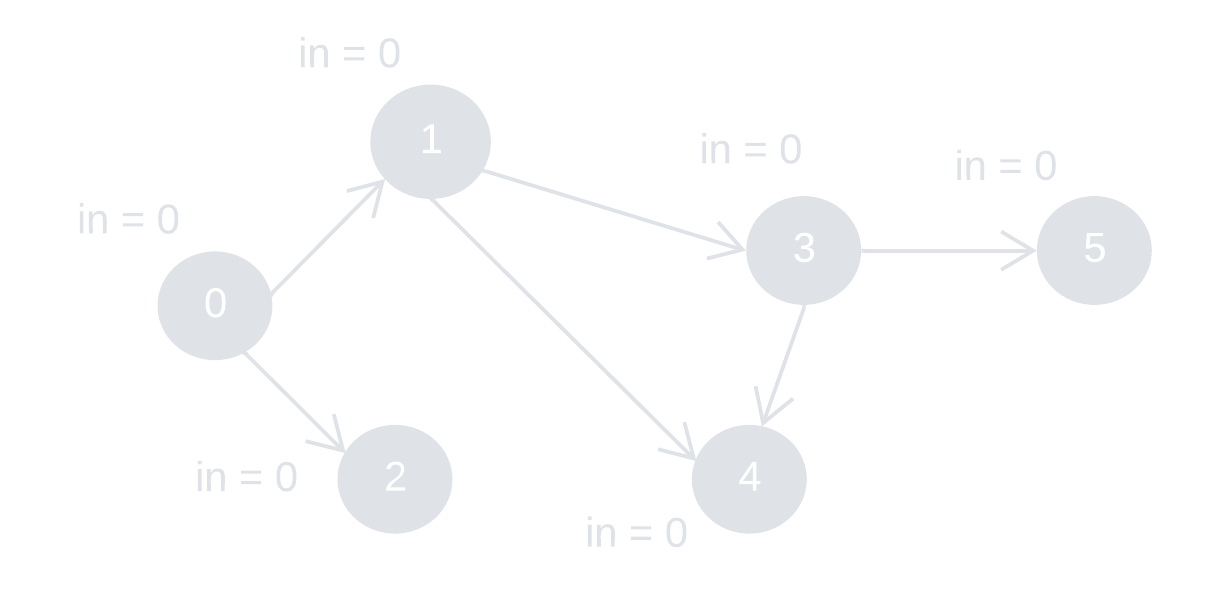
Step 4: remove node 4 and 5.
Given a DAG, denoted as G and represented with an adjacency list, the algorithm can be summarized as follows:
- Calculate the indegree for all nodes in G.
- Identify a node with an indegree of 0, indicating no incoming edges.
- Remove the identified node from G and add it to the topological ordering.
- Remove the outgoing edges from the removed node in G.
- Decrement the indegree of the connected destination nodes (those connected by the edges removed in the previous step).
- Repeat these steps until no nodes are left with zero indegree, signifying that either all nodes have been traversed or a cycle has been encountered.
// pseudo code for an example
Kahn_topological_sort(Graph G)
{
For each node in G{
Find and populate indegree[node]; // get the indegree for all the nodes in G
}
Create a stack or queue; // auxiliary data structure - as a container
Add nodes with indegree 0 to the queue;
while(node U with indegree 0 exists in the queue){
Remove U from the queue;
Remove all its outgoing edges (U, Vi) from G;
For destination vertices Vi which had their incoming edges removed{
indegree[Vi] -= 1;
}
Add new nodes with indegree 0 to the queue;
}
// determine if a topological ordering has been found
if(elements sorted = all elements)
return true or print nodes in topologically sorted order;
else
return false or prompt that no topological ordering exists (e.g. there exists rings in G)
}
Now let's implement it using C++, the very first thing is to design a data structure to store a graph.
For the purpose of simplfying the code, we might as well consider representing the graph nodes using integers, numbering from 0 to a specific value. We can then use these integers as array indices. Consider the following example:
node_array[0] = {1, 2};
To store our graph, we can make use of a 2D array, often referred to as an adjacencyList
vector<vector<int>> adjacencyList;
adjacencyList[0]
represents a 1D array containing the nodes incident to node 0.
The overall code is as follows:
#include <iostream>
#include <vector>
#include <queue>
using std::vector;
using std::queue;
// Graph class - store the input graph
class Graph{
public:
Graph(int NumberOfNodes) : m_numberofNodes(NumberOfNodes){
m_adjacencyList.resize(NumberOfNodes);
m_inDegree.resize(NumberOfNodes, 0);
}
void add_directed_edges(int src, int dest){
m_adjacencyList[src].emplace_back(dest);
}
// main function: topological sort
bool topological_sort(vector<int>& sorted)
{
auto indegree_copy = m_inDegree; // save a copy of the indegree vector
// store all the nodes with no incoming edges
queue nodes_with_zero_indegree;
for(int i = 0; i < m_numberofNodes; ++i)
{
if(m_inDegree[i] == 0)nodes_with_zero_indegree.push(i);
}
// process - while the queue is not empty
while(!nodes_with_zero_indegree.empty())
{
auto current_zero_node = nodes_with_zero_indegree.front();
nodes_with_zero_indegree.pop(); // delete the node with zero indegree
sorted.emplace_back(current_zero_node); // add it to the sorted list
// alter the graph: delete the incident edges and update the indegree
// of the incident nodes connected to current_zero_node
for(auto const& dest_node : m_adjacencyList[current_zero_node])
{
// delete the directed edge: current_zero_node -> dest_node
// meaning the indegree of the dest node decrements by 1
--m_inDegree[dest_node];
// if the updated indegree of dest node is now zero
// add it to the nodes_with_zero_indegree queue
if(m_inDegree[dest_node] == 0) nodes_with_zero_indegree.push(dest_node);
} // end for
} // end while: while the queue is not empty
// a cycle was encountered - if the sorting is done but not all input nodes have been sorted
if((int)sorted.size() != m_numberofNodes)return false;
// successfully sorted
return true;
}
void print_graph() {
for(int i = 0; i < m_adjacencyList.size(); ++i)
{
if(m_adjacencyList[i].size() != 0)
{
std::cout << "Node " << i << " -> ";
for(const auto& node : m_adjacencyList[i])
{
std::cout << node << " ";
}
std::cout << std::endl;
}
}
}
protected:
int m_numberofNodes;
vector<vector<int>> m_adjacencyList;
vector<int> m_inDegree;
};
int main() {
int n = 6;
Graph graph(n);
graph.add_directed_edges(0, 1);
graph.add_directed_edges(0, 2);
graph.add_directed_edges(1, 2);
graph.add_directed_edges(2, 3);
graph.add_directed_edges(1, 4);
graph.add_directed_edges(5, 3);
graph.add_directed_edges(4, 5);
graph.print_graph();
vector<int> sorted;
sorted.reserve(n);
if(graph.topological_sort(sorted)){
std::cout << "sorted done, the topological ordering is: " << std::endl;
for(auto const& node : sorted)std::cout << node << " ";
std::cout << std::endl;
}else{
std::cout << "topological sorting is not possible as the graph is not acyclic" << std::endl;
}
return 0;
}